Binary Morphology: Understanding the Fundamentals

Binary morphological operations form the backbone of many image processing applications. These techniques allow us to manipulate shapes within images, extract important features, and prepare images for further analysis. In this blog post, we’ll explore the core concepts of binary morphology and understand how they can be applied to solve real-world image processing problems.
Introduction to Morphology
Morphology, originally a branch of biology dealing with the form and structure of organisms, has found its way into image processing. In the context of image analysis, morphological image processing refers to operations that extract components for representation and description of region shapes, such as boundaries, skeletons, and convex hulls.
Morphological transformations are primarily performed on binary images (images consisting solely of black and white pixels). These operations require two inputs:
The original image
A structuring element (kernel) that determines the precise nature of the operation
The two foundational morphological operators are Erosion and Dilation, from which we can derive more complex operations like Opening and Closing.
Structuring Elements
Before diving into morphological operations, it’s important to understand what structuring elements are. A structuring element is essentially a shape mask used in basic morphological operations. They can be of any digitally representable shape and size, with common forms including:
Box
Hexagon
Disk
Custom shapes
Each structuring element has an origin, which serves as a reference point when applying the operation.
Binary Morphology
Binary images often suffer from noise (specifically salt and-pepper noise)
Binary regions also suffer from noise (isolated black pixels in a white region). Can also have cracks, picket fence , etc.
Dilation and erosion are two binary morphological operations that can assist with these problems.
Binary Dilation
Dilation is used to expand elements in a binary image. When we dilate an image, we grow the connected sets of 1s (white pixels).
Definition:
Dilation of set A by structuring element B is defined as:
A ⊕ B = { p : such that p = a+b for every a ∈ A and b ∈ B }
In simpler terms, dilation adds pixels to the boundaries of objects in an image.
Example:
Consider an input image A and structuring element B:
A = [0,1], [1,1], [2,1], [2,2], [3,0]
B = [0,0], [0,1]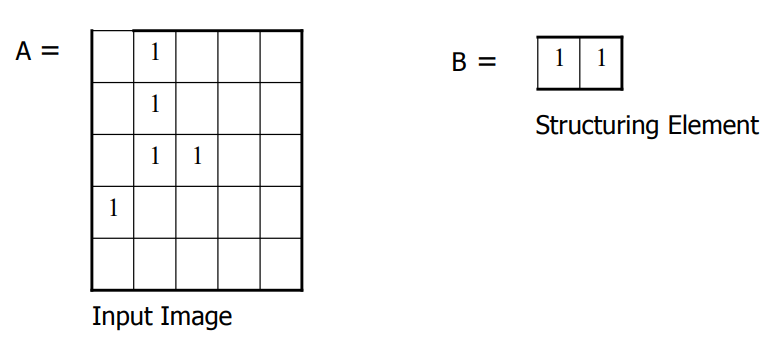
Dilation input image and structuring element
When we perform dilation, we place the origin of B at each pixel in A and include all pixels covered by B in the result. This gives us:
A ⊕ B = [0,1], [1,1], [2,1], [2,2], [3,0], [0,2], [1,2], [2,2], [2,3], [3,1]
Dilation
A ⊕ B =
Dilation Mathematical representation
Visualization:
Dilation visualization
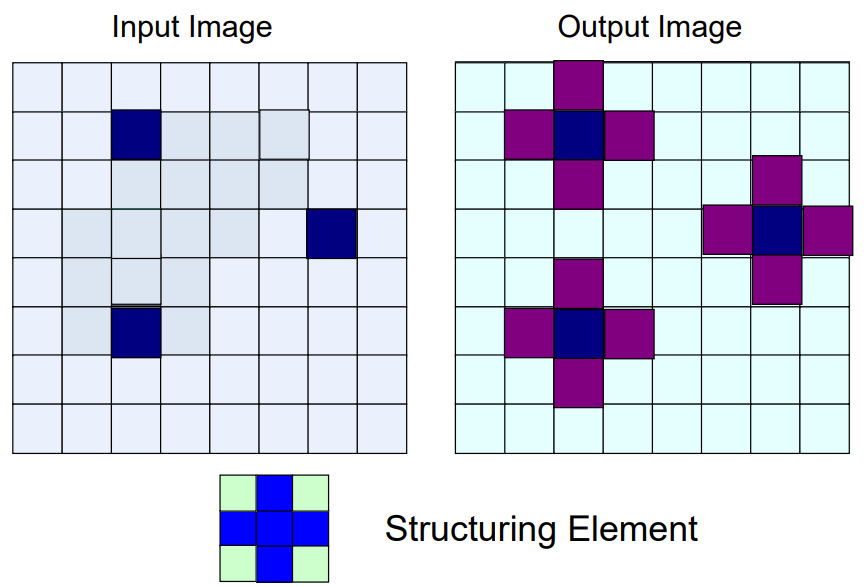
Applications of Dilation:
Expanding features in images
Filling holes and gaps
Smoothing object boundaries
Binary Erosion
Erosion is the counterpart to dilation, used for shrinking elements in a binary image. It removes pixels from the boundaries of objects.
Definition:
Erosion of set A by structuring element B is defined as:
A ⊖ B = { p : such that p+b ∈ A for every b ∈ B }
This means a pixel remains in the eroded image only if the structuring element fits entirely within the object when centered on that pixel.
Example:
Using the same image A and structuring element B as before:
A = [0,1], [1,1], [2,1], [2,2], [3,0]
B = [0,0], [0,1]
Erosion input image and structuring element
When we analyze pixel p = [2,1], we check if all points p+b are in A:
[2,1] + [0,0] = [2,1] ∈ A
[2,1] + [0,1] = [2,2] ∈ A
Since all points are in A, [2,1] remains in the eroded image. When we apply this check to all pixels, only [2,1] satisfies the condition, so:
A ⊖ B = [2,1]
Erosion
Visualization:
Erosion visualization
Conclusion
Binary morphological operations provide powerful tools for analyzing and modifying shapes in binary images. By understanding and applying these morphological operations, we can enhance image quality, extract meaningful features, and prepare images for further analysis in fields like computer vision, medical imaging, document processing, and pattern recognition.
This blog post is based on lecture materials by Dr. Kiran Talele, Associate Professor at Bharatiya Vidya Bhavans’ Sardar Patel Institute of Technology, Mumbai.